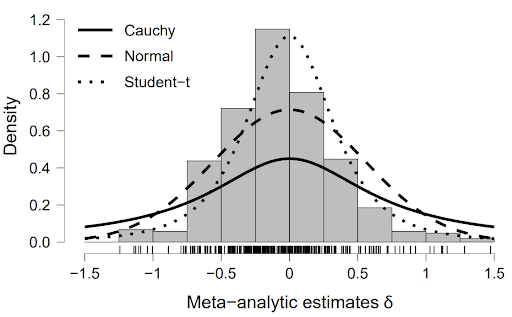
This post is a synopsis of Bartoš, F., Gronau, Q. F., Timmers, B., Otte, W. M., Ly, A., & Wagenmakers, E. J. (2021). Bayesian model‐averaged meta‐analysis in medicine. Statistics in Medicine. The article is available at https://doi.org/10.1002/sim.9170  (open-access).

 

Abstract

We outline a Bayesian model-averaged (BMA) meta-analysis for standardized mean differences in order to quantify evidence for both treatment effectiveness 𝛿 and across-study heterogeneity 𝜏. We construct four competing models by orthogonally combining two present-absent assumptions, one for the treatment effect and one for across-study heterogeneity. To inform the choice of prior distributions for the model parameters, we used 50% of the Cochrane Database of Systematic Reviews to specify rival prior distributions for 𝛿 and 𝜏. The relative predictive performance of the competing models and rival prior distributions was assessed using the remaining 50% of the Cochrane Database. On average, ℋ₁^r —the model that assumes the presence of a treatment effect as well as across-study heterogeneity— outpredicted the other models, but not by a large margin. Within ℋ₁^r , predictive adequacy was relatively constant across the rival prior distributions. We propose specific empirical prior distributions, both for the field in general and for each of 46 specific medical subdisciplines. An example from oral health demonstrates how the proposed prior distributions can be used to conduct a BMA meta-analysis in the open-source software R and JASP. The preregistered analysis plan is available at https://osf.io/zs3df/.

Highlights

In the article we provide an introduction to the Bayesian model-averaged meta-analysis. We further discuss the benefits it brings to medicine, such as a graceful, data-driven transition from fixed- and random-effects:

“An attractive feature of this framework is that it allows a graceful data-driven transition from an emphasis on fixed-effect models to random-effects models; with only few studies available, the fixed-effect models likely outpredict the random-effects models and therefore receive more weight. But as studies accumulate, and it becomes increasingly apparent that the treatment effect is indeed random, the influence of the random-effects models will wax and of the fixed-effect models will wane, until inference is dominated by the random-effects models.”

We assess the relative predictive performance of different prior distributions, and hypotheses, showing that the random-effects model assuming the presence of the effect does not dominate in all cases as widely believed.

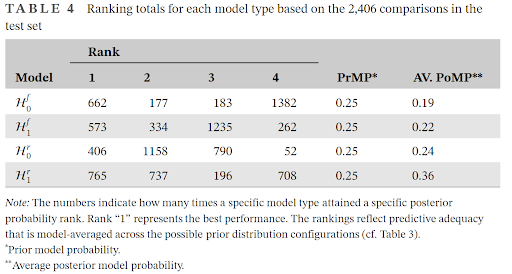
Finally, we develop empirical prior distributions based on the Cochrane Database of System Reviews for meta-analyses of continuous outcomes.

 

About The Authors

František Bartoš

František Bartoš is a PhD candidate at the Psychological Methods Group of the University of Amsterdam.

Quentin Gronau

Quentin is a postdoc at the Psychological Methods Group of the University of Amsterdam.

Wim Otte

Wim Otte is Clinical Epidemiologist and Associate Professor at the Utrecht Medical Center Utrecht.

Bram Timmers

Bram Timmers is a former research master student in psychology at the University of Amsterdam.

Alexander Ly

Alexander Ly is a postdoc at the Psychological Methods Group at the University of Amsterdam.

Eric-Jan Wagenmakers

Eric-Jan (EJ) Wagenmakers is professor at the Psychological Methods Group at the University of Amsterdam.