Here we present a Bayesian analysis of data from a recent labor law case [cc; see also Hummel, 2024]. In the case, several trade unions argued that the Dutch Supreme Court had issued particular judgments (i.e., the “Enerco” judgment from 2014 and the “Amsta” judgment from 2015) that effectively imply legal restrictions on collective actions. The trade unions argue that these restrictions are in violation of European law. Here I will ignore the legal aspects of the case and concentrate solely on the data that the unions presented to bolster their argument. Specifically, we will examine the “number of interim relief judgments in the Netherlands in the five years before and five years after the Enerco/Amsta judgments and the results of those proceedings” (#84 from [cc]). If the unions are correct, the Enerco/Amsta judgments ought to have resulted in a higher proportion of strikes that are prohibited by the judiciary. And indeed, this is what the data appear to show at a first glance:
“Finally also in relative terms a big difference is clearly noticeable. In the 5 years before Enerco/Amsta (partial) prohibitions were imposed by interim relief judges in 44% of cases, compared to 57% after Enerco/Amsta. (…) These figures speak for themselves. The Enerco/Amsta assessment framework has led to a considerable increase in the number of judgments in legal proceedings in which the court imposed restrictions on trade unions taking collective action in the Netherlands.” (#85 from [cc], italics added for emphasis)
In order to assess whether the difference is indeed “big” and “clearly noticeable” we should consider the raw numbers. These are given in the table that accompanies point #84 in [cc]. The table shows that pre-Enerco/Amsta, 15 out of 27 collective actions were allowed (56%) which dropped to 14 out of 33 (42%) post-Enerco/Amsta. Do these numbers warrant the conclusion that the Enerco/Amsta rulings imply legal restrictions on collective actions? In what follows I will take a statistical approach to address this question.
Why Statistics?
A popular objection to the use of statistics in scenarios such as these is that “the entire population has been sampled”: we have observed all of the available cases and hence there are no other cases to which we would like to generalize. For the present scenario I believe this argumentation to be fallacious. In this case the skeptical position is that the Enerco/Amsta judgments had no impact of the restrictions on collective actions imposed by the courts. The position from the unions is that the Enerco/Amsta judgments did have such an effect, which is offered as a causal explanation for the observed data. We wish to use grade the evidence that the observed data provide for the causal claim, and this can happen irrespective of the size of the underlying population — for our beliefs about the plausibility of the causal claim it does not matter that there would or would not be unobserved cases. All that matters is the data that have been obtained. In order to gauge the evidence that the data provide for and against the union claim we now turn to a Bayesian analysis.
The Model
For the analysis of the data I will use a Bayesian comparison of two proportions (e.g., Gronau et al., 2021; Kass & Vaidyanathan, 1992). The model is a dummy-coded logistic regression where the test-relevant parameter ψ equals the log odds ratio, which is assigned a normal prior: ψ ~ N(μ,σ). Consider the following three models:
- “H0: ψ = 0”: the null hypothesis that the Enerco/Amsta judgments did not affect verdicts;
- “H+: ψ > 0”: the hypothesis that the Enerco/Amsta judgments increased the tendency to permit actions;
- “H-: ψ < 0”: the hypothesis that the Enerco/Amsta judgments decreased the tendency to permit actions.
Model H- is the one put forward by the unions. Model H+ is included for completeness, but also because it was relatively plausible a priori, as indicated in the union report for the court:
“(…) it had been expected by the trade unions that the change in the Supreme Court case law would lead to broadening the scope in Dutch case law for taking collective actions.”(#84 from [cc]; italics added for emphasis)
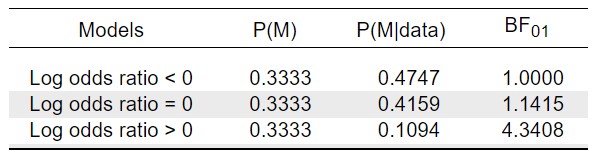
Each of the three models is given equal prior probability. The models H+ and H- feature a standard normal prior, truncated to respect directionality; H+: ψ ~ N+(μ=0,σ=1) and H-: ψ ~ N-(μ=0,σ=1). The results are obtained with a few mouse clicks in JASP, and are provided in the table below:
The data warrant only a modest update of the prior probabilities. The model H- that the Enerco/Amsta judgments decreased the tendency to permit actions receives most support from the data, but only 1.14 times as much as the null hypothesis (this is shown in the column BF01, which indicates the Bayes factor in favor of the top model to the models in each of the rows; the Bayes factor quantifies the degree to which one model outpredicts another, Jeffreys, 1939). This is a clear case of “absence of evidence“. Even the hypothesis H+ that the Enerco/Amsta judgments actually increased the tendency to permit actions retains a posterior probability of 11% and can therefore not be ruled out with much confidence. As an aside, the frequentist p-value equals .31, providing no indication whatsoever that the null hypothesis should be rejected.
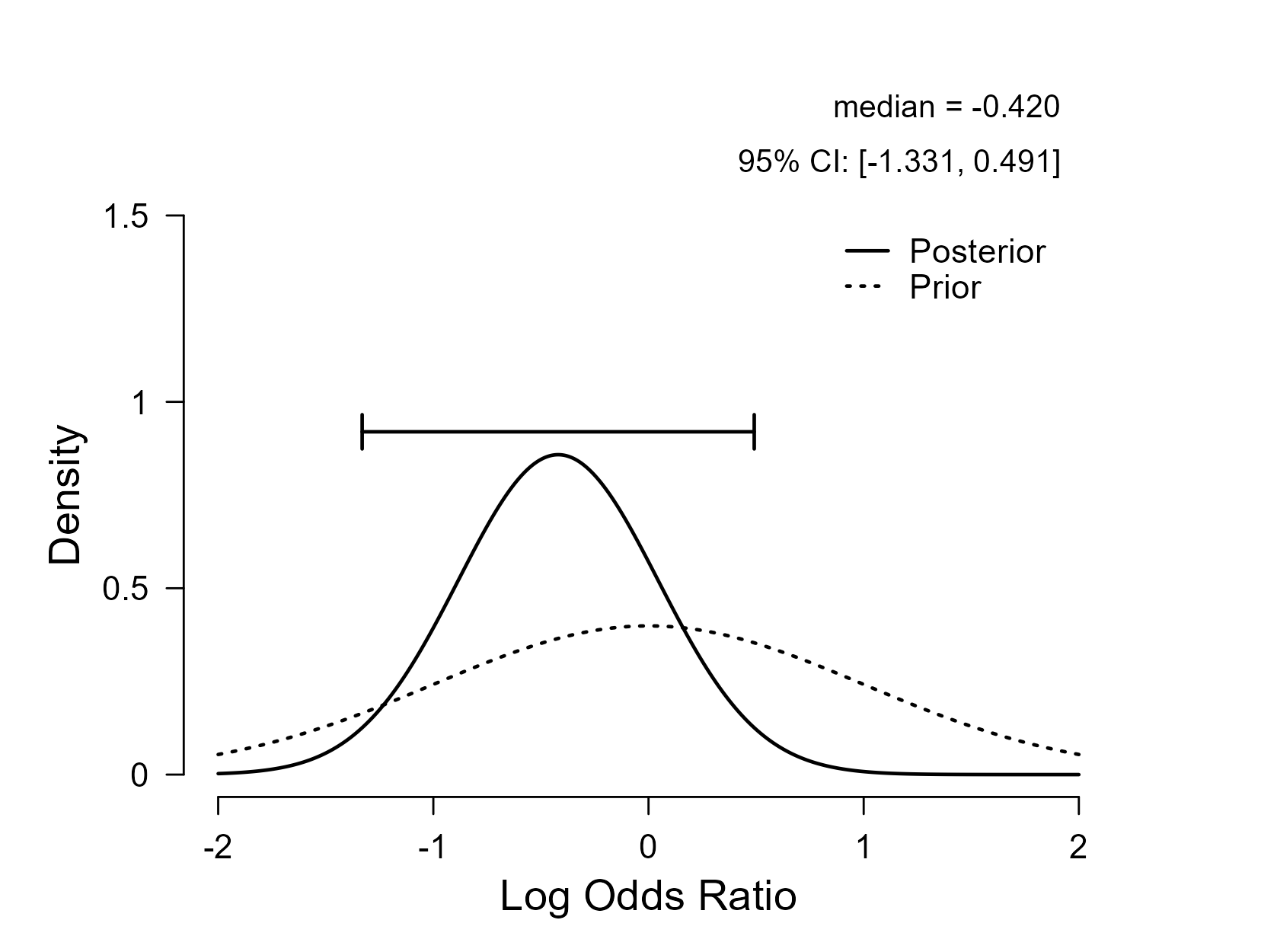
For completeness, below is the prior and posterior distribution for ψ under the model that assigns it an untruncated standard normal distribution, that is, H1: ψ ~ N(μ=0,σ=1):
It is clear that the posterior distribution is relatively wide, that a considerable portion of it is allocated to positive values of ψ, and that the change from prior to posterior is relatively modest. These results do not seem to warrant the kind of strong statements presented in the union report.
Robustness Check
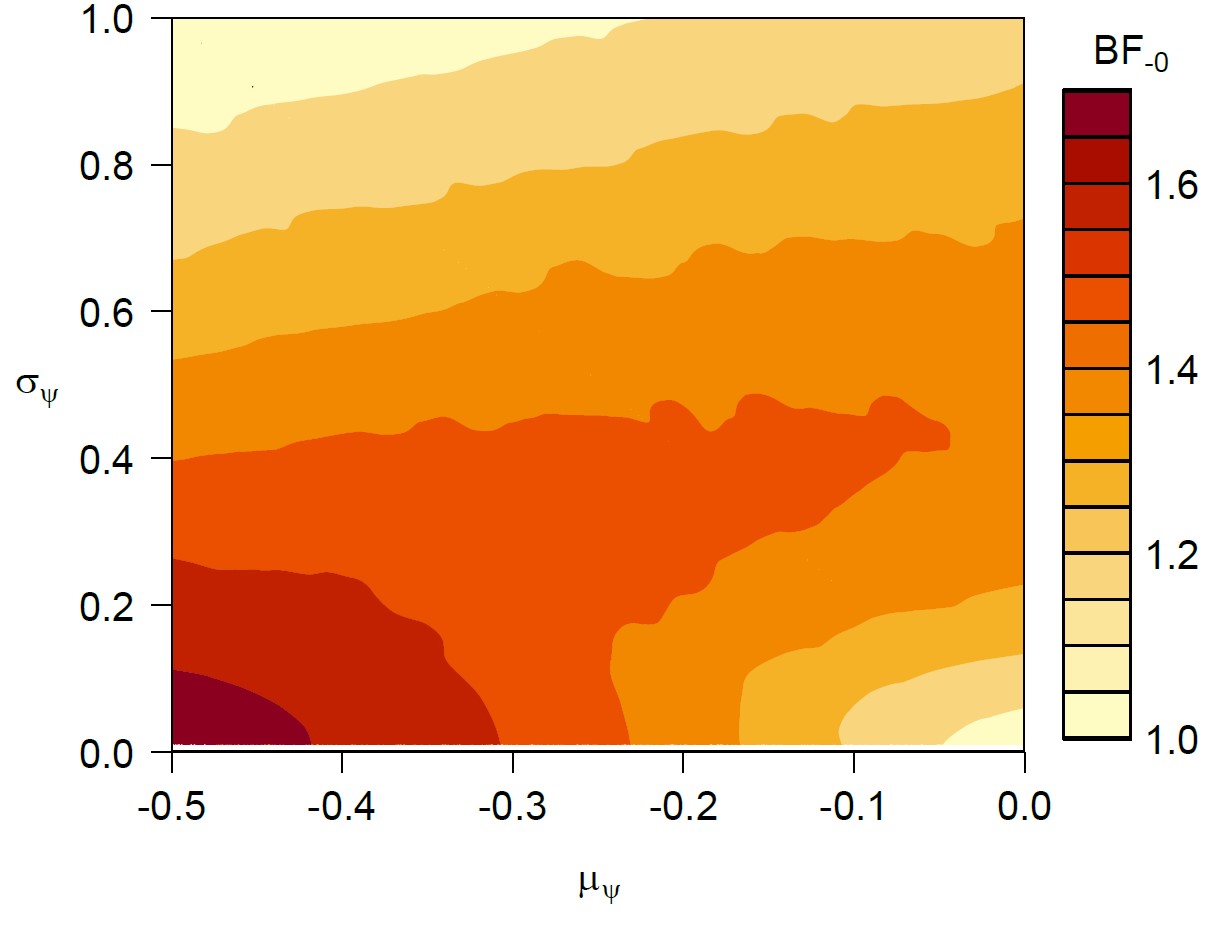
In order to assess the robustness of the above conclusion we focus on the two models that received the most support from the data, that is, H0 and H-. In JASP a comprehensive robustness check can be executed with a single mouse click. This robustness check yields a landscape of Bayes factors as a function of changing both the location μ and the width σ of the normal prior distribution on the log odds ratio ψ. The figure below shows the landscape that results when the location μ is varied from 0 to -0.5, and and the width σ is varied from 0 to 1. The main information is provided by the scale of the legend: the Bayes factors are never compelling, and only exceed 1.5 in a small part of the space. Generally, reasonable changes in the prior distribution do not alter the main conclusion, namely that the data show absence of evidence.
The Ruling
In 2024, the European Committee of Social Rights issued a ruling, which took into account both the quantitative and qualitative analyses presented by the unions. In this ruling, they rejected the claim by the unions, siding squarely with the Dutch government:
Having considered all the arguments presented by the parties, the Committee maintains its assessment made in Conclusions 2018 (see above) and considers that the framework laid down by the Supreme Court through the Enerco and Amsta judgments recognises the intrinsic link between collective bargaining and collective action, it expressly provides that the scope for collective action should not be interpreted narrowly, and it moderates the role that the rules of the game used to play in court decisions concerning whether or not to permit collective action. Consequently, the Supreme Court’s assessment framework does, as such, not infringe the right of workers’ and employers’ organisations to take collective action.” (#93 from [dm], italics in original)
General Advice for Presenting Quantitative Information in Court
The proper interpretation of quantitative data demands a quantitative analysis. Data do not speak for themselves, but need to be interpreted with the help of a statistical model. Before presenting quantitative findings to the court, advice ought to be sollicited from a statistician, and preferably a Bayesian one :-).
References
Hummel, N. (2024). De Raad van Europa en (ambtenaren)stakingen. Tijdschrift voor Ambtenarenrecht, 62.
Kass, R.E., & Vaidyanathan S. K. (1992). Approximate Bayes factors and orthogonal parameters, with application to testing equality of two binomial proportions. Journal of the Royal Statistical Society: Series B (Methodological), 54, 129-144.
Gronau Q. F., Raj K. N. A., & Wagenmakers E.-J. (2021). Informed Bayesian inference for the A/B test. Journal of Statistical Software, 100, 1-39.
Jeffreys, H. (1939). Theory of Probability (1st ed.). Oxford: Oxford University Press.