This post is a synopsis of Bartoš, F, Maximilian M, Wagenmakers E.-J., Doucouliagos H., & Stanley, T D. (2021). No need to choose: Robust Bayesian meta-analysis with competing publication bias adjustment methods. Preprint available at https://doi.org/10.31234/osf.io/kvsp7
Abstract
“Publication bias is a ubiquitous threat to the validity of meta-analysis and the accumulation of scientific evidence. In order to estimate and counteract the impact of publication bias, multiple methods have been developed; however, recent simulation studies have shown the methods’ performance to depend on the true data generating process – no method consistently outperforms the others across a wide range of conditions. To avoid the condition-dependent, all-or-none choice between competing methods we extend robust Bayesian meta-analysis and model-average across two prominent approaches of adjusting for publication bias: (1) selection models of p-values and (2) models of the relationship between effect sizes and their standard errors. The resulting estimator weights the models with the support they receive from the existing research record. Applications, simulations, and comparisons to preregistered, multi-lab replications demonstrate the benefits of Bayesian model-averaging of competing publication bias adjustment methods.”
Highlights
“Kvarven et al. (2020) compared the effect size estimates from 15 meta-analyses of psychological experiments to the corresponding effect size estimates from Registered Replication Reports (RRR) of the same experiment. RRRs are accepted for publication independently of the results and should be unaffected by publication bias. This makes the comparison to RRRs uniquely suited to examine the performance of publication bias adjustment methods. Kvarven et al. (2020) found that conventional meta-analysis methods resulted in substantial overestimation of effect size. In addition, Kvarven et al. (2020) examined three popular bias detection methods: trim and fill (TF; Duval and Tweedie, 2020), PET-PEESE (Stanley & Doucouliagos, 2014), and 3PSM (Hedges, 1992; Vevea & Hedges, 1995).”
Kvarven et al (2020) conclude “We furthermore find that applying methods aiming to correct for publication bias does not substantively improve the meta-analytic results. The trim-and-fill and 3PSM bias-adjustment methods produce results similar to the conventional random effects model. PET-PEESE does adjust effect sizes downwards, but at the cost of substantial reduction in power and increase in false-negative rate. These results suggest that statistical solutions alone may be insufficient to rectify reproducibility issues in the behavioural sciences[…]”
While this limitation seems to apply to previous statistical methods the new implementation of RoBMA is much more accurate on RRRs.
“The main results are summarized in Table 2. Evaluated across all metrics simultaneously, RoBMA-PSMA and RoBMA-PP generally outperform the other methods. RoBMA-PSMA has the lowest bias, the second-lowest RMSE, and the second lowest overestimation factor. Similarly, RoBMA-PP has the fourth-best bias, the lowest RMSE, and the fourth-best overestimation factor. The only methods that perform better in one of the categories (i.e., AK2 with the lowest overestimation factor; PET-PEESE and EK with the second and third lowest bias, respectively), showed considerably larger RMSE, and AK2 converged in only 5 out of 15 cases. Furthermore, RoBMA-PSMA and RoBMA-PP resulted in conclusions that are qualitatively similar to those from the RRR studies.”
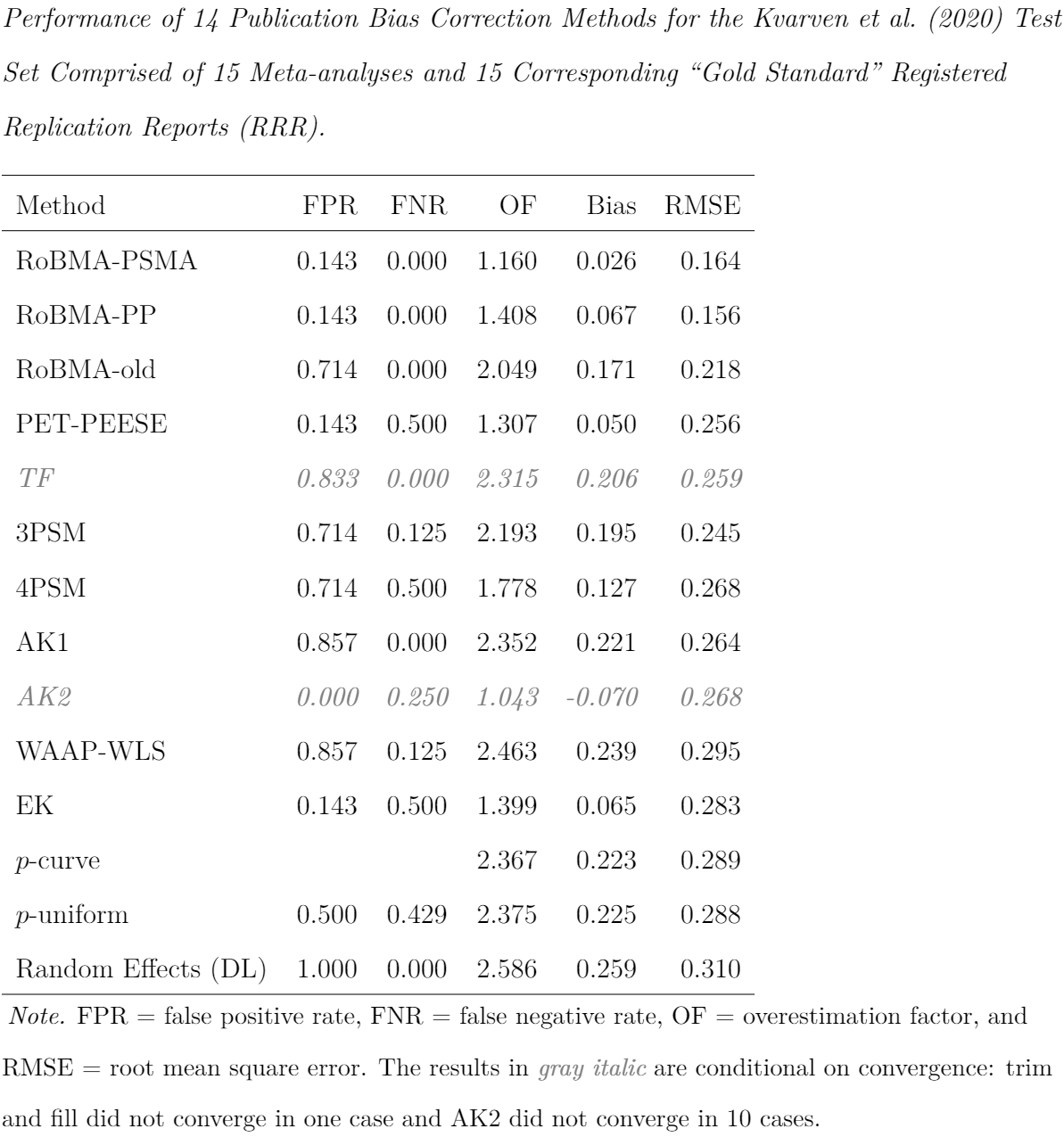
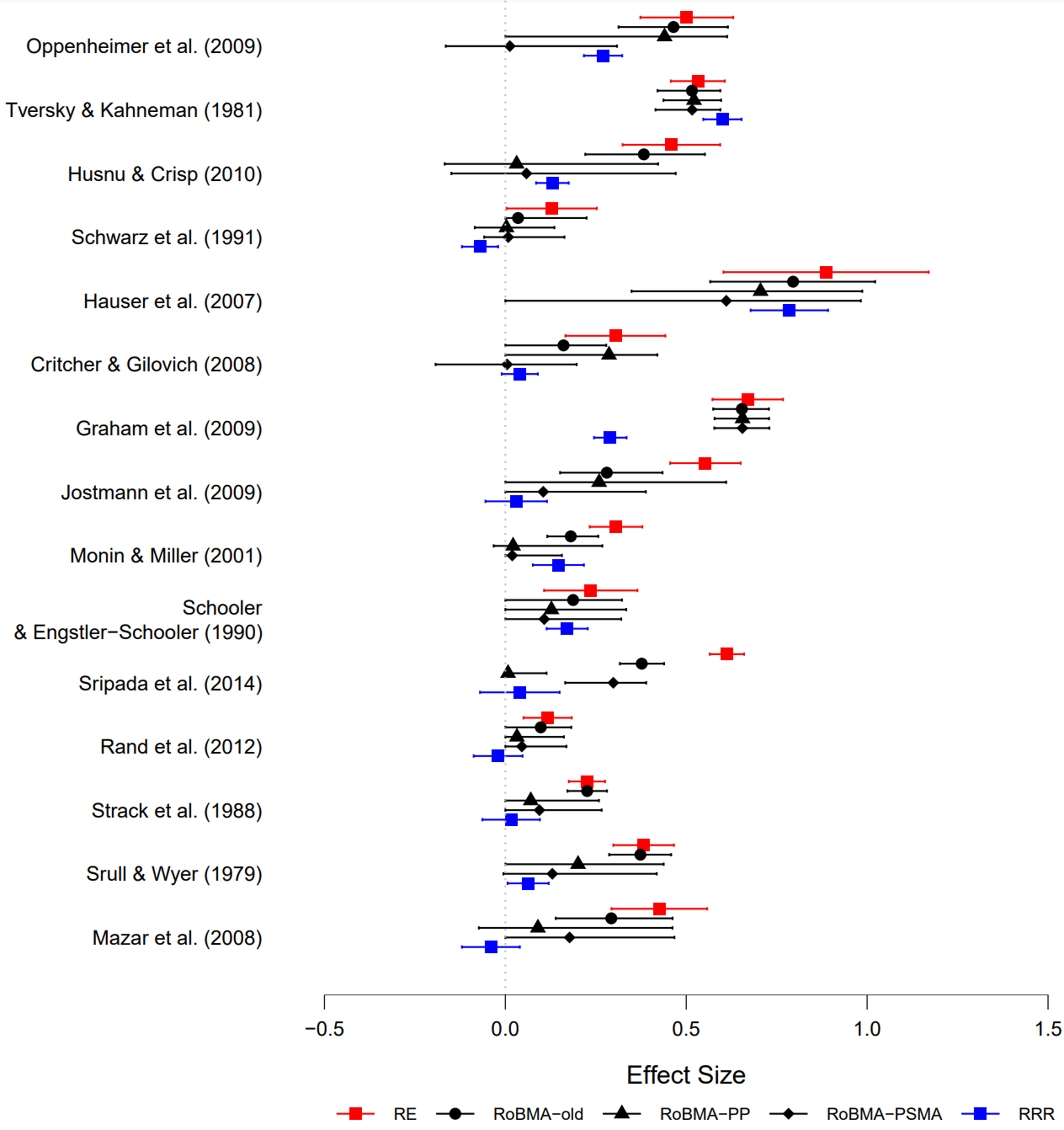
“Figure 3 shows the effect size estimates from the RRRs for each of the 15 cases, together with the estimates from a random effects meta-analysis and the model-averaged estimates from RoBMA, RoBMA-PSMA, and RoBMA-PP. Because RoBMA-PSMA and RoBMA-PP correct for publication bias, their estimates are shrunken toward zero. In addition, the estimates from RoBMA-PSMA and RoBMA-PP also come with wider credible intervals (reflecting the additional uncertainty about the publication bias process) and are generally closer to the RRR results.”
References
Duval, S., & Tweedie, R. (2000). Trim and fill: A simple funnel-plot–based method of testing and adjusting for publication bias in meta-analysis. Biometrics, 56 (2), 455–463. https://doi.org/10.1111/j.0006-341X.2000.00455.x
Hedges, L. V. (1992). Modeling publication selection effects in meta-analysis. Statistical Science, 7 (2), 246–255.
Kvarven, A., Strømland, E., & Johannesson, M. (2020). Comparing meta-analyses and preregistered multiple-laboratory replication projects. Nature Human Behaviour, 4(4), 423–434. https://doi.org/10.1038/s41562-019-0787-z
Stanley, T. D., & Doucouliagos, H. (2014). Meta-regression approximations to reduce publication selection bias. Research Synthesis Methods, 5(1), 60–78. https://doi.org/10.1002/jrsm.1095703
Vevea, J. L., & Hedges, L. V. (1995). A general linear model for estimating effect size in the presence of publication bias. Psychometrika, 60 (3), 419–435. https://doi.org/10.1007/BF02294384
About The Authors

František Bartoš
František Bartoš is a Research Master student in psychology at the University of Amsterdam.

Maximilian Maier
Maximilian Maier is a Research Master student in psychology at the University of Amsterdam.

Eric-Jan Wagenmakers
Eric-Jan (EJ) Wagenmakers is professor at the Psychological Methods Group at the University of Amsterdam.

Chris Doucouliagos
Chris Doucouliagos is a professor of meta-analysis at Deakin Laboratory for the Meta-Analysis of Research (DeLMAR), Deakin University. He is also a Professor at the Department of Economics at Deakin.

Tom Stanley
Tom Stanley is a professor of meta-analysis at Deakin Laboratory for the Meta-Analysis of Research (DeLMAR), Deakin University. He is also a Professor at the School of Business at Deakin.


