In a recent article for Computational Brain & Behavior, we discussed several limitations of Bayesian leave-one-out cross-validation (LOO) for model selection. Our contribution attracted three thought-provoking commentaries by (1) Vehtari, Simpson, Yao, and Gelman, (2) Navarro, and (3) Shiffrin and Chandramouli. We just submitted a rejoinder in which we address each of the commentaries and identify several additional limitations of LOO-based methods such as Bayesian stacking. We focus on differences between LOO-based methods versus approaches that consistently use Bayes’ rule for both parameter estimation and model comparison.
We conclude that (1) LOO-based methods such as Bayesian stacking do not align satisfactorily with the epistemic goal of mathematical psychology; (2) LOO-based methods depend on an arbitrary distinction between parameter estimation and model comparison; and (3) LOO-based methods depend on an arbitrary distinction between data that arrive sequentially or “simultaneously”. In line with Lewandowsky and Farrell (2010) we believe that careful model comparison requires both quantitative evaluation and intellectual and scholarly judgment. We personally prefer quantitative evaluation of models based on consistently using Bayes’ rule for both parameters and models (e.g., via the Bayes factor). This approach has the advantage that, in line with the epistemic purpose of mathematical psychology, it enables the quantification of evidence for a set of competing theories that are implemented as quantitative models. Researchers may criticize the specification of an ingredient of Bayes’ rule such as the prior distribution for a particular application. However, once the ingredients have been specified, there is only one optimal way of updating one’s knowledge in light of observed data: the one that is dictated by Bayes’ rule. Alternative methods may be useful in specific circumstances and for specific purposes but –as we illustrated with the case of LOO– they will break down in other settings yielding results that can be surprising, misleading, and incoherent.
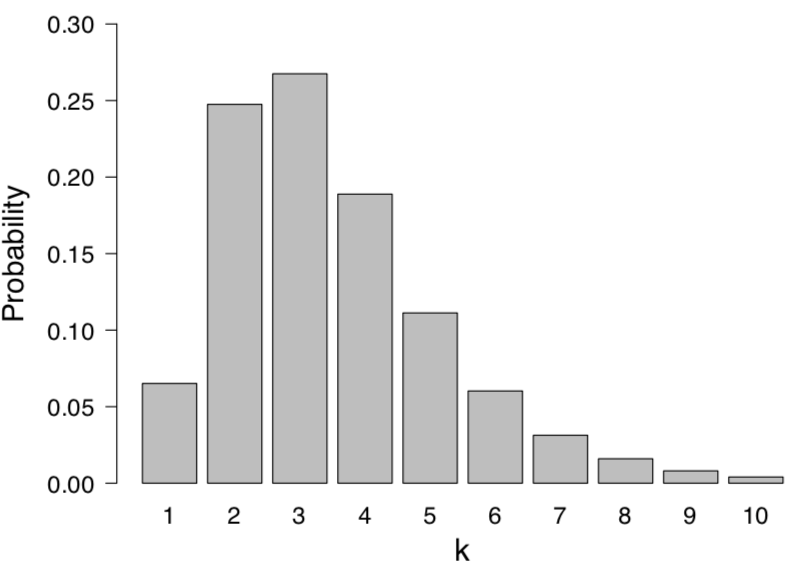
Figure 1. Parameter estimation or model comparison? Shown is the posterior distribution for the tumor transplant example based on 1 “take” out of 6 attempts and a uniform prior for k, the number of genes determining transplantability. Here k may be regarded as a parameter, such that the depicted distribution is a parameter posterior distribution, or k may be regarded as indexing separate models, so that the depicted distribution corresponds to posterior model probabilities. Available at https://tinyurl.com/y94uj4h8 under CC license.
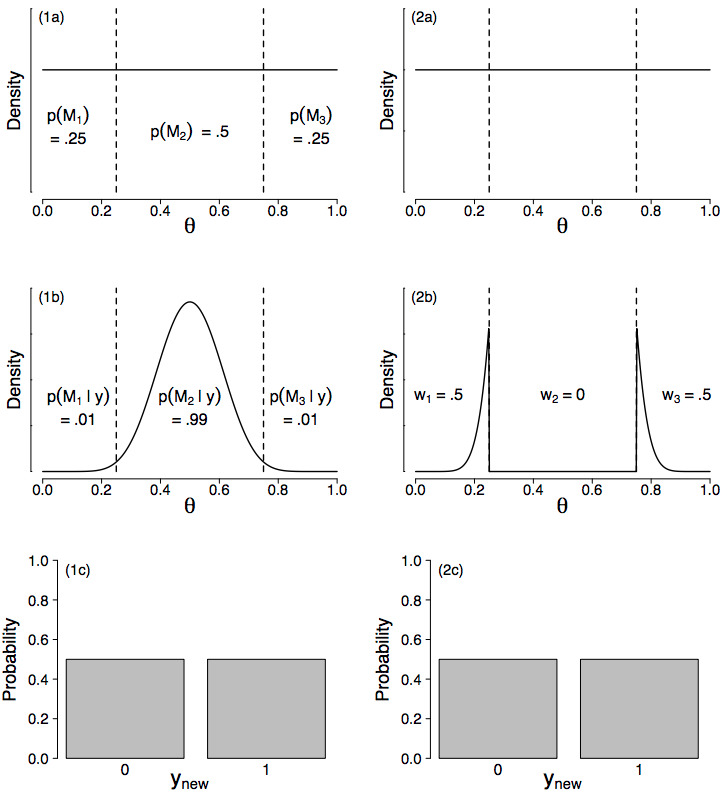
Figure 2. BMA (left column) and Bayesian stacking (right column) results for the Bernoulli example based on 10 successes out of n = 20 observations. Panels (1a) and (2a) show the uniform prior distribution for 
References
Gronau, Q. F., & Wagenmakers, E.-J. (2018). Rejoinder: More Limitations of Bayesian leave-one-out cross-validation. Manuscript submitted for publication and uploaded to PsyArXiv.
Gronau, Q. F., & Wagenmakers, E.-J. (in press). Limitations of Bayesian leave-one-out cross-validation for model selection. Computational Brain & Behavior.
Lewandowsky, S., & Farrell, S. (2010). Computational modeling in cognition: Principles and practice. Thousand Oaks, CA: Sage.
Navarro, D. J. (in press). Between the devil and the deep blue sea: Tensions between scientific judgement and statistical model selection. Computational Brain & Behavior.
Shiffrin, R. M., & Chandramouli, S. H. (in press). Commentary on Gronau and Wagenmakers. Computational Brain & Behavior.
Vehtari, A., Simpson, D. P., Yao, Y., & Gelman, A. (in press). Limitations of “Limitations of Bayesian leave-one-out cross-validation for model selection”. Computational Brain & Behavior.
About The Authors
Quentin Gronau
Quentin is a PhD candidate at the Psychological Methods Group of the University of Amsterdam.
Eric-Jan Wagenmakers
Eric-Jan (EJ) Wagenmakers is professor at the Psychological Methods Group at the University of Amsterdam.
