Some time ago I ran a twitter poll to determine what people believe is the best statistics book of all time. This is the result:

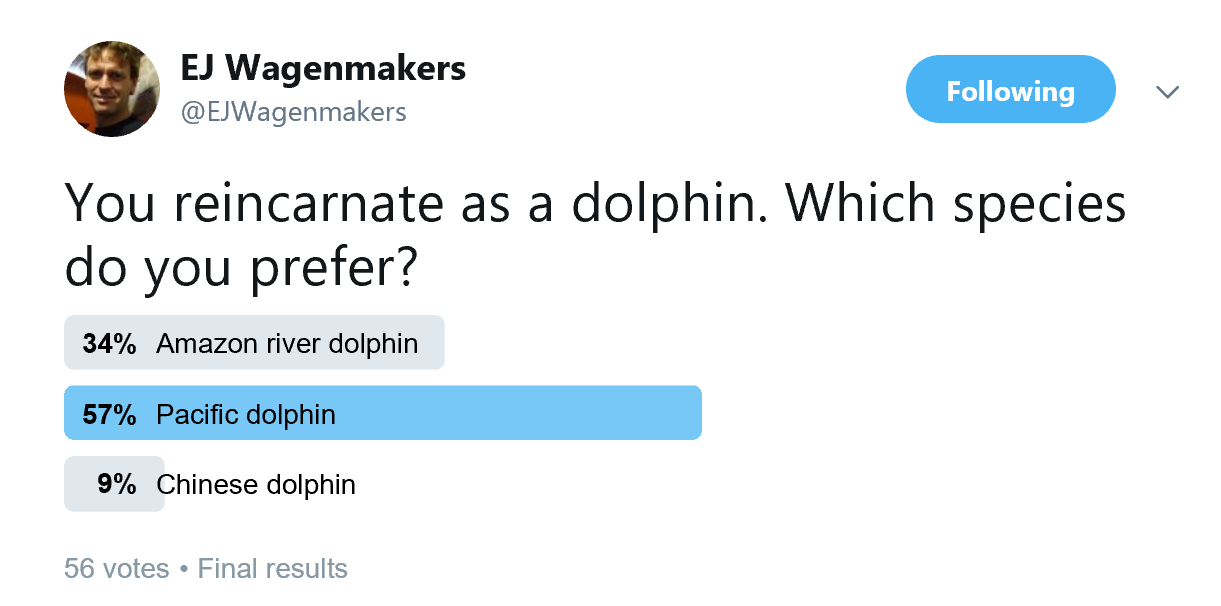
The first thing to note about this poll is that there are only 26 votes. My disappointment at this low number intensified after I ran a control poll, which received more than double the votes:

If I had to vote in my own book poll I probably would pick the 3rd edition of Theory of Probability (1961) as the best, because it is the most complete. But an argument can be made that the 1st edition (1939) is intellectually the most impressive achievement.
Unfortunately, ToP is not only the best book about statistics that is ever written, it is also tremendously challenging to grasp in its entirety. A complete understanding is probably only feasible for the Roberts, Bergers, and Gelmans of this world, but I suspect that even they would find certain sections tough going. Jeffreys was a great writer, but he did not like to belabor what to him was obvious. And his notation is both archaic and idiosyncratic, easily wrong-footing the modern reader. But those who persist will discover that almost every page presents an absolutely crucial insight. Just to list a few examples, Jeffreys offers transformation-invariant priors, solves the problem of induction inherent to the Bayes/Laplace approach, develops concrete Bayesian tests for popular statistical scenarios, discusses what is now known as the Lindley paradox (well before Lindley), critiques the frequency interpretation of probability, and offers a definition of the p-value that is correct, amusing, and damning all at the same time:

“What the use of P implies, therefore, is that a hypothesis that may be true may be rejected because it has not predicted observable results that have not occurred. This seems a remarkable procedure.” (Jeffreys, 1961, p. 385, italics in original)

As a whole, ToP represents a monumental effort to construct a method of scientific learning that is fundamentally sound but also practically relevant. From the preface to the first edition: “The chief object of this work is to provide a method of drawing inferences from observational data that will be self-consistent and can also be used in practice.” In my opinion, the contents of ToP has lost none of its relevance for modern empirical research — the main difficulty is that the work is not communicated through R code and Shiny apps; in the pre-computer era, Jeffreys instead presented a deluge of analytic expression and approximations. I believe the book would have much more impact if the derivations had been relegated to appendices. To Jeffreys, however, the details of the derivations were often important, so perhaps there is no getting around them.

A modern discussion of ToP can be found in Robert et al. (2009) and Ly et al. (2016). In the next years, the JASP team will continue to unlock Jeffreys’s statistical legacy for empirical researchers and present Bayesian inference alongside frequentist inference.

References

Jeffreys, H. (1939). Theory of Probability. Oxford: Oxford University Press.

Jeffreys, H. (1948). Theory of Probability (2nd ed.). Oxford: Oxford University Press.

Jeffreys, H. (1961). Theory of Probability (3rd ed.). Oxford: Oxford University Press.

Ly, A., Verhagen, A. J., & Wagenmakers, E.-J. (2016). Harold Jeffreys’s default Bayes factor hypothesis tests: Explanation, extension, and application in psychology. Journal of Mathematical Psychology, 72, 19-32.

Robert, C. P., Chopin, N., & Rousseau, J. (2009). Harold Jeffreys’s Theory of Probability revisited. Statistical Science, 24, 141-172.

About The Authors

Eric-Jan Wagenmakers

Eric-Jan (EJ) Wagenmakers is professor at the Psychological Methods Group at the University of Amsterdam.